This post assumes a passing familiarity with what a Distinguishing Attack on a cryptographic hash is, as well as the high level composition of Bitcoin block headers and mining them.

tldr:
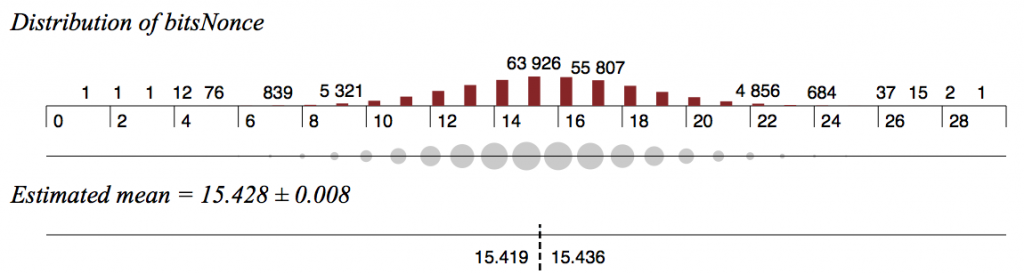
To distinguish between an ideal random permutation hash and SHA256, hash a large amount (~2^80) of candidate 1024 bit blocks twice, as done in Bitcoin. Ensure that the bits of the candidate blocks are sparsely set (much fewer than the 512 mean expected), according to the Bitcoin protocol, discarding candidate blocks that do not meet the Bitcoin “difficulty” standard (where the resultant hashes start with a the large number of 0’s). With the remaining set of valid input candidates (467369 when this analysis was done), observe a particular set of 32 bits in the input block (located where Bitcoin has the nonce, input bits 607-639). Note that the mean number of bits set in the nonce field is skewed to the left, i.e. fewer than the expected value of 16 bits set (estimated mean 15.428).

What is happening to cause this? It is probably caused by the fact that the sparsity of bits set in the input to the SHA256 hashes coupled with the particular selection of outputs (also with fewer bits set than the expected mean) resulted in a bias towards even fewer bits in the input values. Since the nonce (and in a lesser manner, time and Merkle root) are the main variables in selecting the “winning” blocks, this results in fewer bits set in the nonce than random chance would explain.

What the nonce distribution looks like:

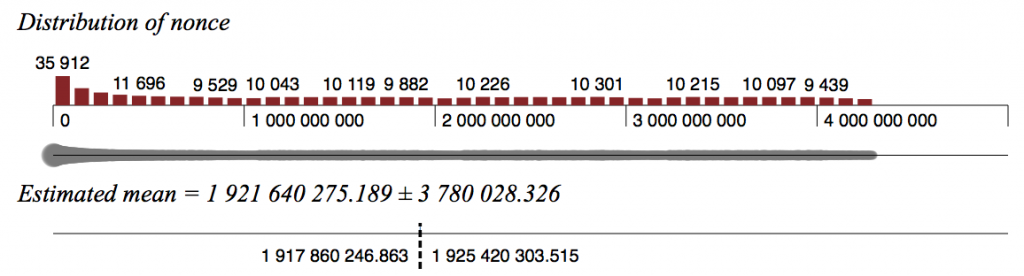
But is this not just caused by Benford’s Law?

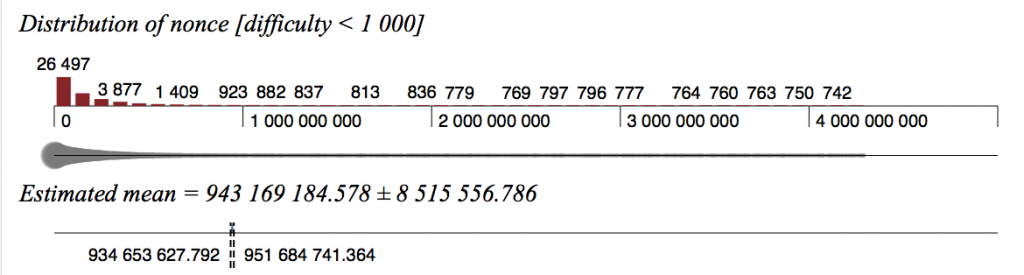
Initially, yes – a study of mining code shows that the early versions reset the nonce to 0 every time a valid block was found, but later optimisations (speed is everything) removed that extra instruction, as it served no real purpose. This can be clearly seen when graphing nonce distribution for the early blocks (difficulty < 1000) compared to later, when the difficulty reached 1000.

Early block nonces for difficulty < 1000 (count 82656):

Block nonces for difficulty >= 1000 (count 384713):

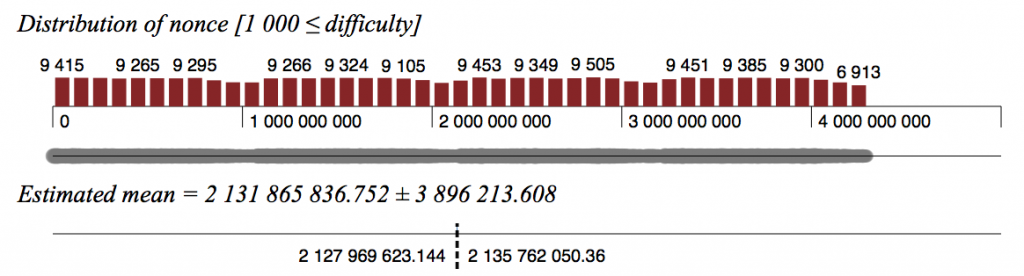
The nonces in this later set follow a much flatter distribution, and if they were randomly chosen, for a set this large, the expected mean number of bits set in the 32 bit nonces should be extremely close to 16. The actual mean number of bits set is 15.701, which a highly significant deviation from the expected value:

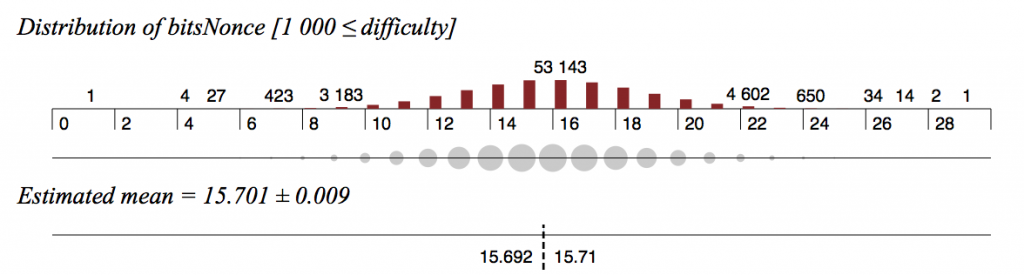
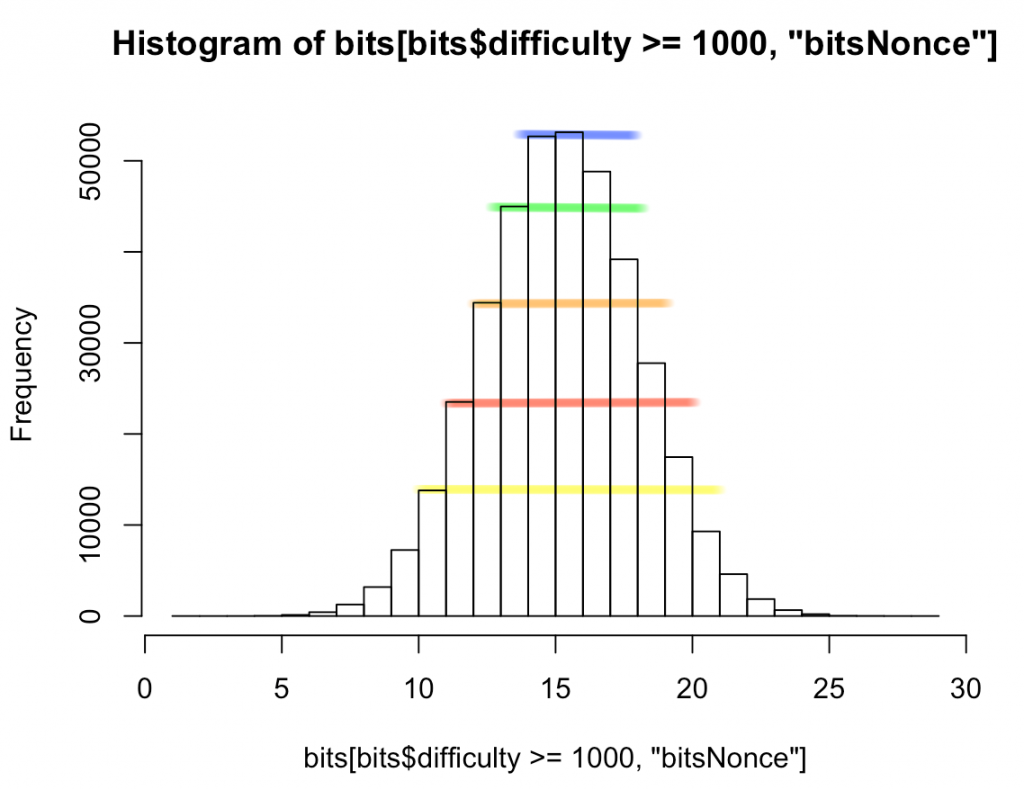
Not only are fewer bits set than expected, but the entire histogram is skewed, with the left shoulder of each partition of bits being significantly taller than the corresponding shoulder to the right of the expected mean of 16, as shown in this next image:

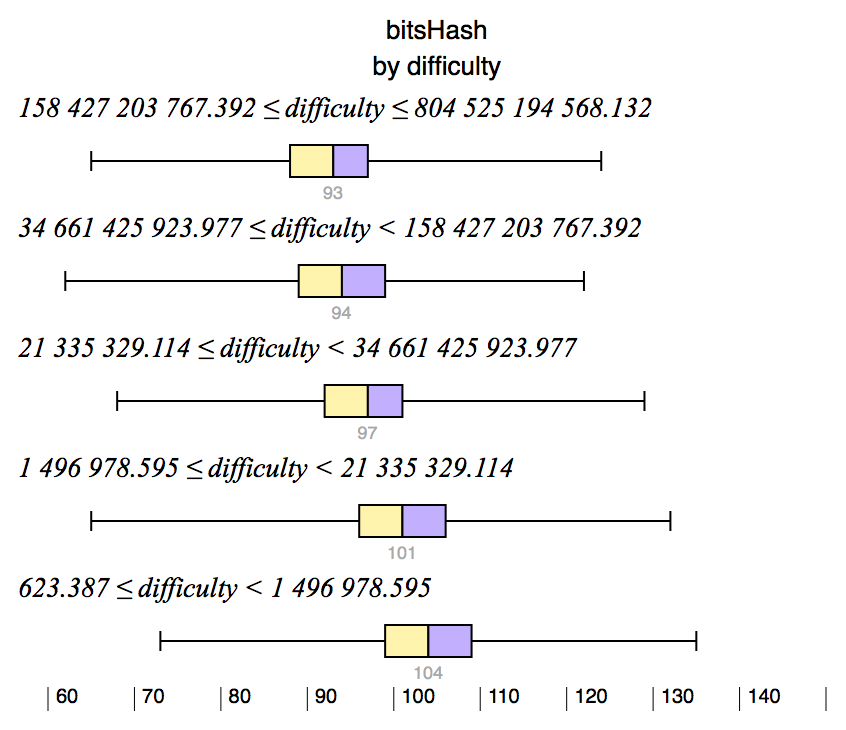
As the difficulty increases, more and more 0s are needed in the final hash, and as expected, the number of bits set in the final output hash reduces:

Studying the values of the individual bits making up the nonces is even more interesting. To appreciate the effect, here is what the value of the LSB of the time value looks like as the difficulty increases:

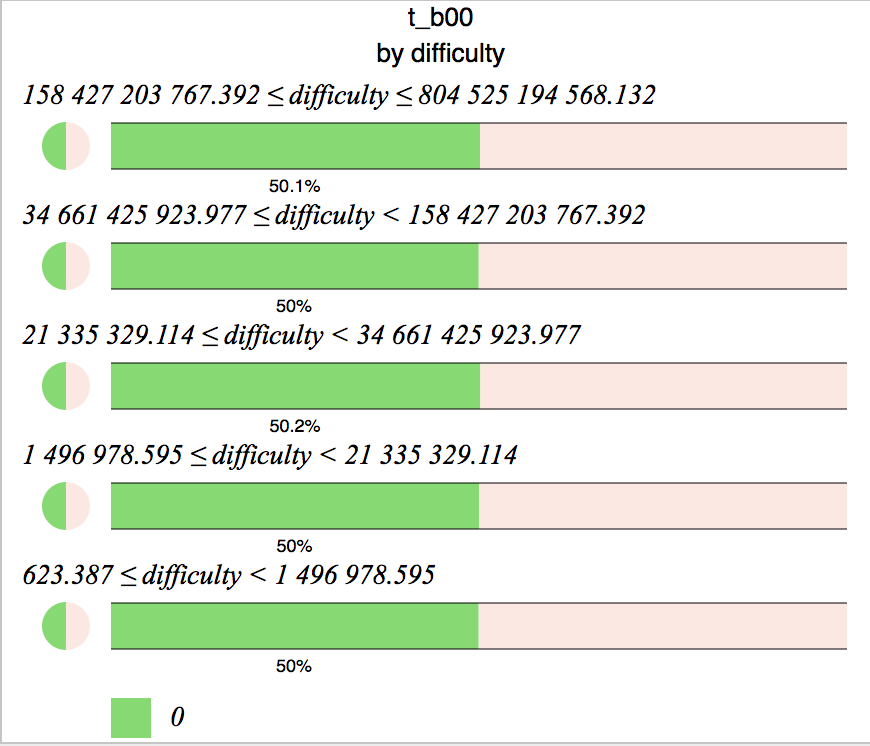
As expected, 50% 0, 50% 1, very boring.

Here is the same graph for bit 7 of the nonce:

Overall, for difficulty values of 1000 and more, 55.9% of the time bit 7 of the nonce is a 0. Other notable nonce bits and the percentage of time they are 0 (more than 52.5%):
Bit 5: 52.9%
Bit 6: 54.6%
Bit 7: 55.9%

Only 3 bits are 0 less than 50% of the time, and the lowest value is 49.8%.
This even correlates further: In a large random sample, the expected number of times 2 bits would both be 0 is 25%. Even knowing the above percentages would still underestimate the incidence of 0: both bits 6 and 7 of the nonce are expected to be 0 at the same time 30.5% given the above stats, yet the actual incidence is 30.7%. Add bit 5, (3 bits would give an expected percentage of 12.5%, with the above percentages, 16.2%) and the incidence is 17%!

What does this imply for Bitcoin mining? Well, a quick test would be to not try nonces where bits 5,6 or 7 are set to 1. This will result in mining 8 times “faster”, as 87.5% of candidates will not be checked, but will still hit 17% of valid hashes – a 36% speedup in terms of hashing effort expended vs hashes found. It is also fast to check for this in code with a bitmask. If anyone tries this, and it works, donations can be sent here: 1Mk7r7Ubim4auUuZudqamWR8beavWaJN5

Takeaways:

• Given two black boxes, one being a random 256-bit permutation, the other being SHA256, it is possible to distinguish between them using carefully constructed input and about 2^80 hashes.
• It should be possible to mine Bitcoin faster, thereby increasing profits.