In 2023 we, the training team within Orange Cyberdefense and specifically Ulrich Swart, Matthew Hughes and myself, attempted to do something a little different for Black Hat with regards to our in class competition.
Each year we give a select few students some swag for portraying the most “plakker” mindset, being active in class, or finding another method to solve the practical.
The concept we decided to explore that year was creating a deck of standard playing cards they could bring out when friends are over and become a discussion point. The cards have educational tidbits about some material they will learn on some of our flagship courses, specifically the Infrastructure, Web Application, Wi-Fi and Red Team courses each had their own suit.
When we had come up with some core ideas we went to Andre for the final approval, and he said, “Yes but there needs to be easter eggs”.
This was 2 weeks before the FINAL print design needed to be submitted. Ulrich rushed to get a bunch of visual easter eggs into the cards, I won’t tell you all of them but they include pictures of our old shirts, training badges and more. See if you can spot them?
And on the box we added an encoded version of Dan Geer’s famous saying we continue to live by.
Lastly we added a little two step CTF – Despite adding the CTF page link (https://t.ly/BdBsx) and in binary form (of the link) onto the back of the cards for printing, I only created the actual challenges while our team was flying to Vegas.
I managed to send the first challenge to Ulrich while he was at his layover in Atlanta.
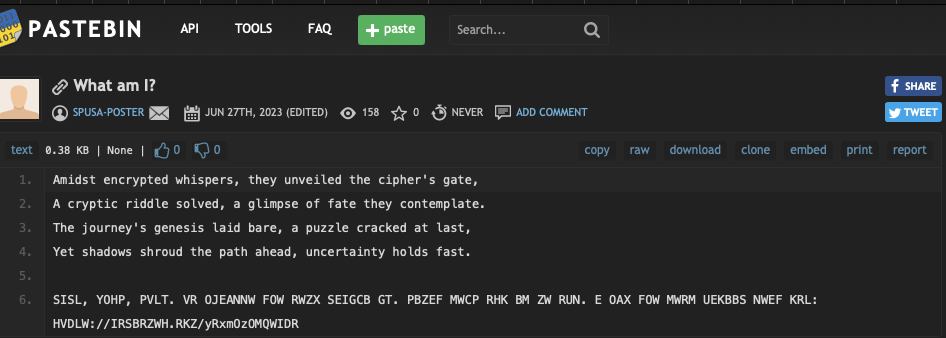
Having decoded the binary back to ASCII, we will receive a pastebin link. From here you will be presented with a lovely poem (thoughtfully written by ChatGPT) and some sort of encrypted text. By its intention and design it’s pretty easy to see it is a cipher, from the HVDLW://IRSBRZWH.RKZ/yRxmOzOMQWIDR which appears to follow the structure of a URL. However “HVDLW” cannot be a simple shift otherwise VD would be the same letters being that it comes from TT, if we assume its HTTPS. This rules most basic ciphers like Caesar and ROT13.
What we’re looking for is something that shifts each letter differently, a polyalphabetic substitution if you will. One such example of this is a Vignear Cipher. It takes a key and applies that key across the string. For example if you have a key KEY and a string you wish to encrypt “My Secret” the first letter “M” will be shifted by K letters the Y by E, S by Y and E by K and so on. resulting in “Cu Uuytup”.
So we want to make HTTPS at some point so we could try understand what letters would help us recreate this but as this is a CTF its likely the clue is hidden somewhere.
On the back on the cards and large in your face on the front of the box the phrase “WE HACK WE TRAIN YOU PWN” could be found. If we put that into CyberChef we see that it was the code.
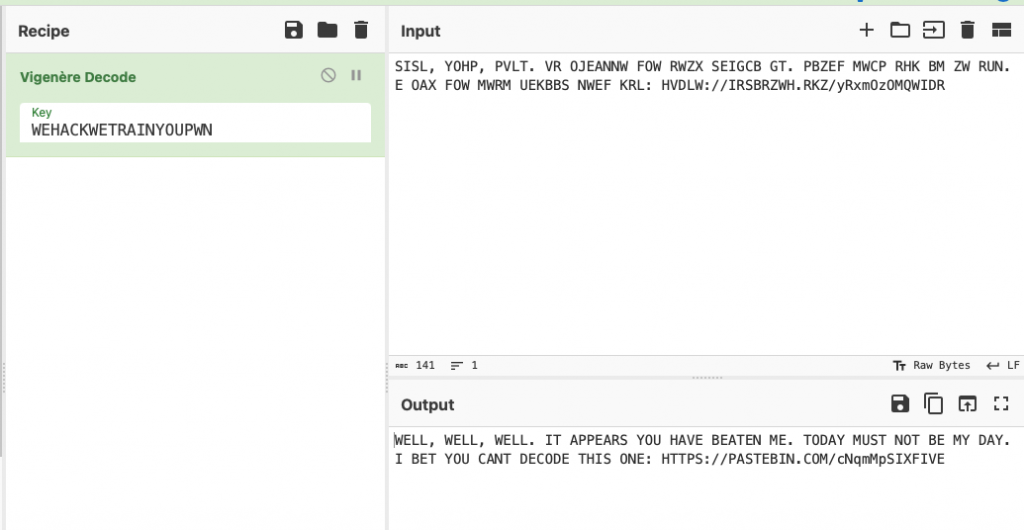
This directs us to the next pastebin location.
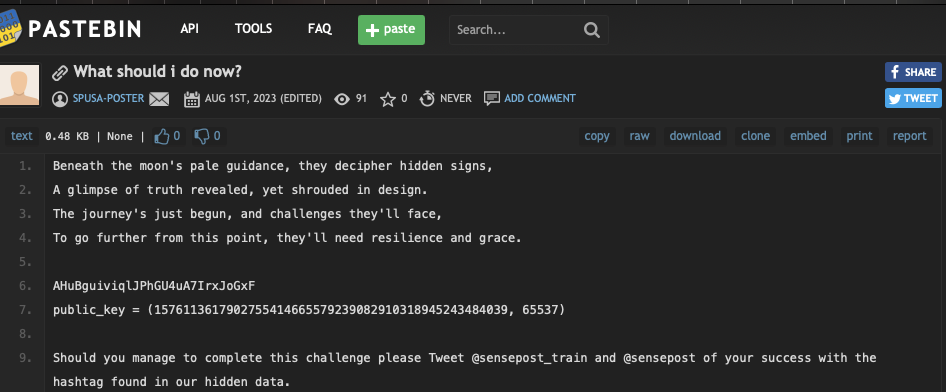
More poems (more thank you’s to ChatGPT), some garbage looking string and a public key. To the observant you will straight away notice the sting is likely to be base64 encoded.

But if we do decode it, it’s more garbage. Most likely whatever this garbage is, its an encrypted string using the given public key. So we need to find the private key.
Creating RSA keys is a relatively easy but interesting process. We need to provide three prime numbers, two of which will be used to create a modulus (N) and one will be used as an encryption exponent (e). Commonly the exponent is 65537.
The first two prime numbers (p, q) are multiplied together creating N. We then need to create Euler’s Totient of the modulus (N), noted by the greek word phi (?). Phi is the breakability of a number, I.E. how many integers share a common factor with a given number. phi is generally difficult to calculate except in the case of prime numbers as prime numbers share no common factors therefore phi of a prime number (p) is equal to p-1. Phi is also multiplicative therefore if we want to know the value of phi(N), we know N = p*q so phi(N) = phi(p*q) = phi(p) * phi(q)
Therefore phi(N) = (p-1)*(q-1).
Next we find the decryption exponent (d) by finding the modular inverse of the exponent given phi(N). You’ll then use these numbers to generate a public key given the Modulus (N) and exponent (e) and generate the private key using the decryption exponent (d) and modulus (N).
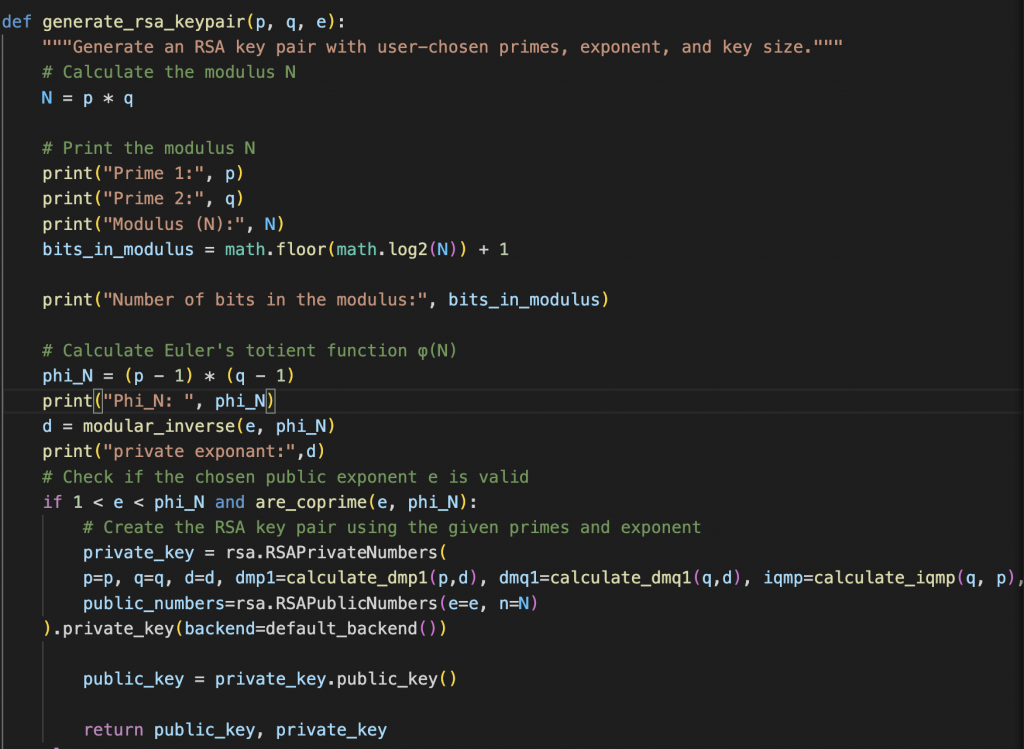
So back to the challenge – given what we now know, it’s obvious we have been given the public key with (modulus, exponent). Therefore, we should be able to figure out how the modulus was calculated and we could retrace the steps to create the decryption exponent and then create a matching private key.
This was the trickiest part as it is computationally difficult to find the the two prime numbers. I used sympy’s factorint function which returns “a dictionary containing the prime factors of n as keys”.
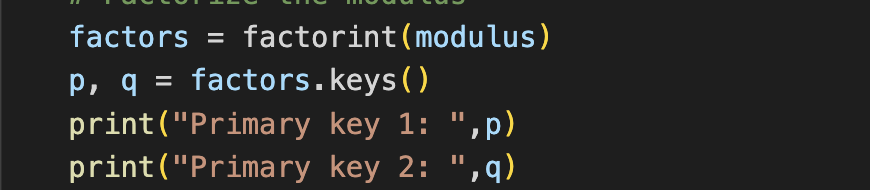
From there it’s as simple as recreating the decryption key and regenerating a private key to decrypt the garbage hidden in the base64 encoded string. Simplified how that’ll look:


What was nice to see was that people were playing – during Black Hat alone we saw that 36 people made it to the second page with @SoSogum3 finishing the challenge first.
Incredibly, since then we are still seeing people playing the game. In the last week alone I have seen 8 new visits to the final challenge page.
I would like to thank ChatGPT for its poem and for fixing bugs in my code. To create and recreate RSA keys you can use my crappy code:
https://gitlab.sensepost.com/jason.spencer/rsa-keys-ctf





