I created a small crypto style CTF for Black Hat last year (we’re training again this year, check our courses out) and hid the starting point in an “easter egg” on a deck of cards. The deck of cards are a custom design by the SensePost training team, which were themed around hacking and were handed out during the conference. This post covers how we built it, and how to solve it.
Amongst several easter eggs, Ulrich put into the deck a binary string for which the translated version of that text was https://t.ly/BdBsx. This t.ly link was to be the start of the CTF. Just before we sent it to print, I had no idea what CTF I was going to build but I said to Ulrich, “Print, I’ll figure out where it goes later”.

Being the serial procrastinator that I am, I left it to just about the last possible second and while the team was flying to Las Vegas, I set out to create something cool.
I managed to send the first challenge to Ulrich while he was at his layover in Atlanta. Having decoded the binary to readable text or by directly using the shortened link, we would get a PasteBin link with the following contents:
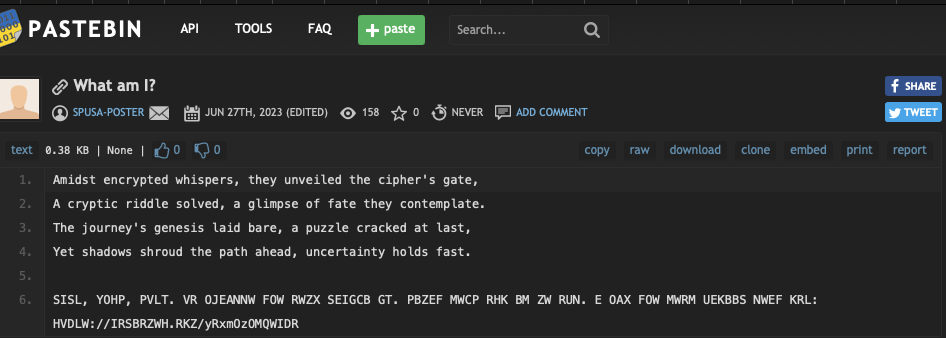
A lovely poem (thoughtfully written by ChatGPT) followed by some sort of encrypted text. By design, it’s pretty easy to see it is a cipher, from the HVDLW://IRSBRZWH.RKZ/yRxmOzOMQWIDR which clearly appears to be a URL. If we assume, that the “HVDLW” represents “HTTPS”, then it cannot be a simple shift otherwise the “VD” would be the same letters being that it represents the “TT”. This rules out most basic ciphers like Caesar and ROT13.
What we’re looking for is something that shifts each letter differently, a polyalphabetic substitution, if you will. One such example of this is a Vigenère cipher – it takes a key and applies that key across a target string. For example, if you have a key KEY and a string you wish to encrypt “My Secret” the first letter “M” will be shifted by K letters, the Y by E, S by Y and E by K and so on.
Assuming HTTPS is correct, we need to figure out what the key is to decrypt this. As this is a CTF its likely the clue is hidden somewhere. On the back of the cards and large in your face on the front of the box the phrase “WE HACK WE TRAIN YOU PWN” could be found. If we put that into CyberChef, we see that it was the key.
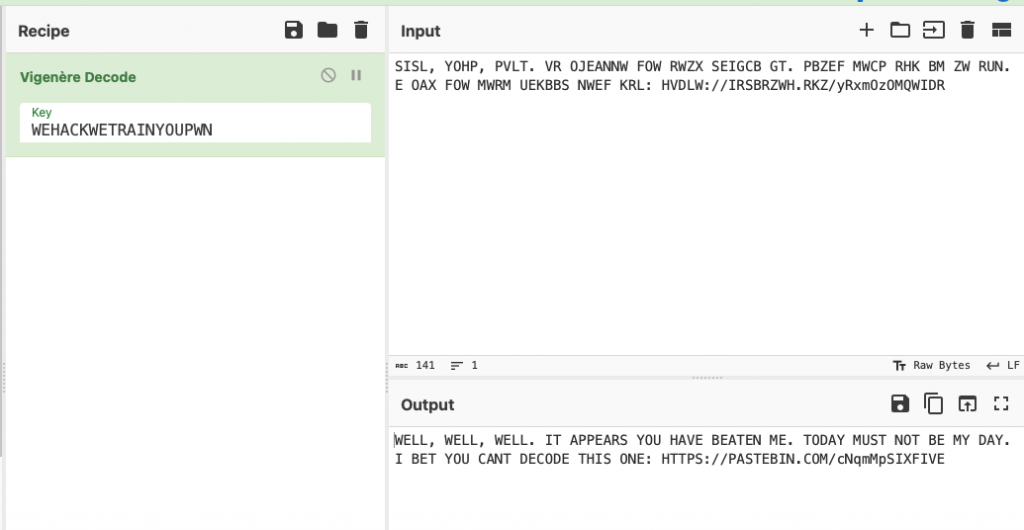
This directs us to the next PasteBin location.
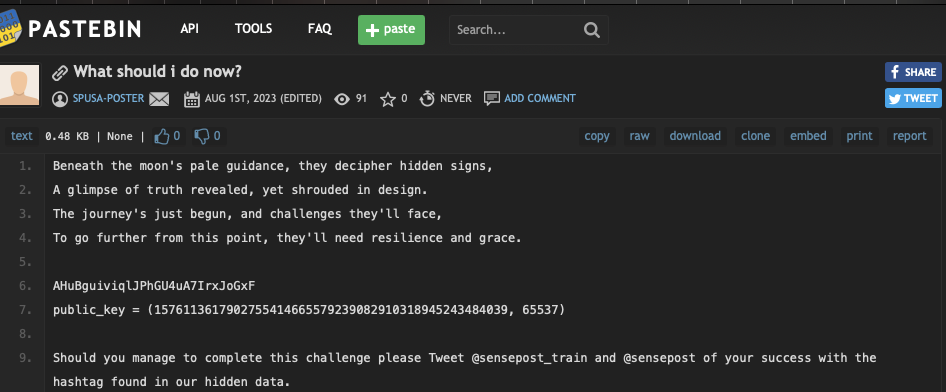
More poems (more thank yous to ChatGPT), some garbage looking string and a public key. To the observant, you will immediately notice the string is likely to be base64 encoded.

But if we do decode it, it’s more garbage. Most likely whatever this garbage is, its an encrypted string using the public key given.
How does the Whole public private key thing work?
In layman’s term, if someone (say Mike) wants to send me something private they can ask for my public key. The public key is, well, public, and can be shared with anyone. Mike can then use my public key to encrypt their data and send that encrypted data to me. I store my private key securely on my personal device and should be the only one that has access to that. I can then use that private key (which corresponds with the public key I shared), to decrypt the message Mike has sent me. The public key is fine to share, provided that is, the key is significantly long. In practice this can be achieved using RSA encryption. Let’s take a look at how RSA keys are created.
Creating RSA keys is a relatively easy, but interesting process. We need to provide three prime numbers, two of which will be used to create a modulus (N) and one of which will be used as an encryption exponent (e). Commonly the exponent is 65537. The first two prime numbers (p, q) are multiplied together creating N.
In order to get two prime numbers I chose two “small” prime numbers found a random number between those and used SymPy’s nextprime function to find the next available prime number. This allowed me to generate different keys each time I would want to create a set of keys while also creating weak RSA keys that was big enough to encrypt the data.
We then need to create Euler’s totient of the modulus (N) noted by the greek word “phi”. “phi” is the breakability of a number, i.e., how many integers share a common factor with a given number. “phi” is generally difficult to calculate except in the case of prime numbers as prime numbers share no common factors. As a result, the phi of a prime number (p) is equal to p-1 (see Khan Academy for math lessons).
Referencing the linked Khan Academy lesson we learn that “phi” is also multiplicative, meaning if we want to know the value of phi(N)
we know N=p*q so phi(N) = phi(p*q) = phi(p) * phi(q). Therefore phi(N) = (p-1)*(q-1). Next, we find the decryption exponent (d) by finding the modular inverse of the exponent given phi(N).
More Khan Academy math teaches us that the inverse of a number (N) is 1/N. For modular inverse we do not have division, however we do have inverses.
The modular inverse of A (mod C) is A^-1. We need to find the B value where B*A mod C = 1. In our case this means we need to find a number B where B*e mod(phi(N)) =1. This can be done a couple of different ways. For larger numbers you can use the extended Euclidean algorithm but for smaller numbers like we have here we can use built in functions such as python’s pow function.
You’ll then use these numbers to generate a public key given the modulus (N) and exponent (e) and generate the private key using the decryption exponent (d) and modulus (N).
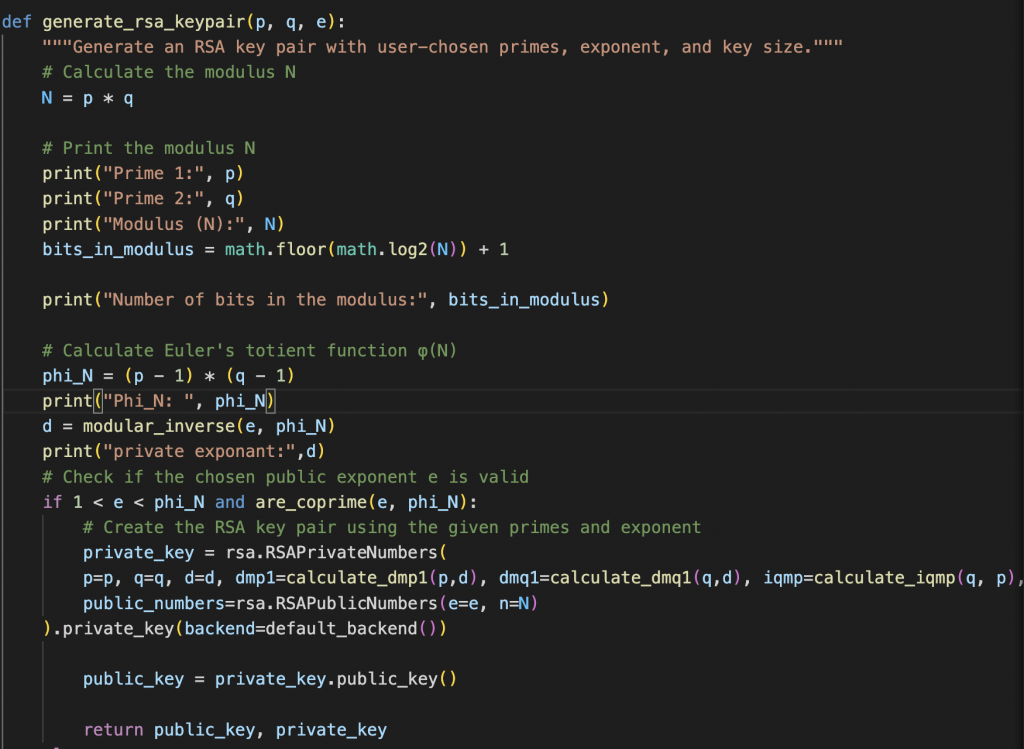
So back to the challenge: Given what we now know, it’s obvious we have been given the public key with (modulus, exponent). Therefore, should we be able to figure out how the modulus was calculated, meaning that we could retrace the steps to create the decryption exponent and then create a matching private key. This was the trickiest part as it is computationally difficult to to find the the two prime numbers. I used SymPy’s factorint function which returns “a dictionary containing the prime factors of n as keys.”
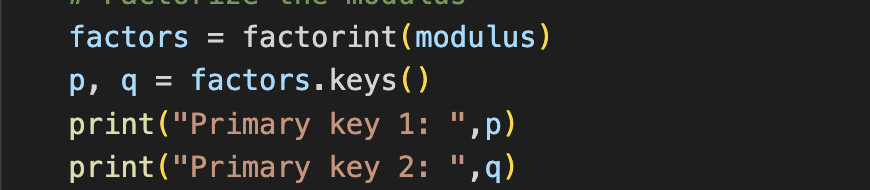
From there it’s as simple as recreating the decryption key and regenerating a private key to decrypt the garbage hidden in the base64 encoded string. Simplified, that will look something like this:


I would like to thank ChatGPT for its poem and for fixing bugs in my code. To create and recreate RSA keys you can use my not so great code.


